Part I (Permainan Set)

21:46:00   Cap Set

Sederhananya begini:

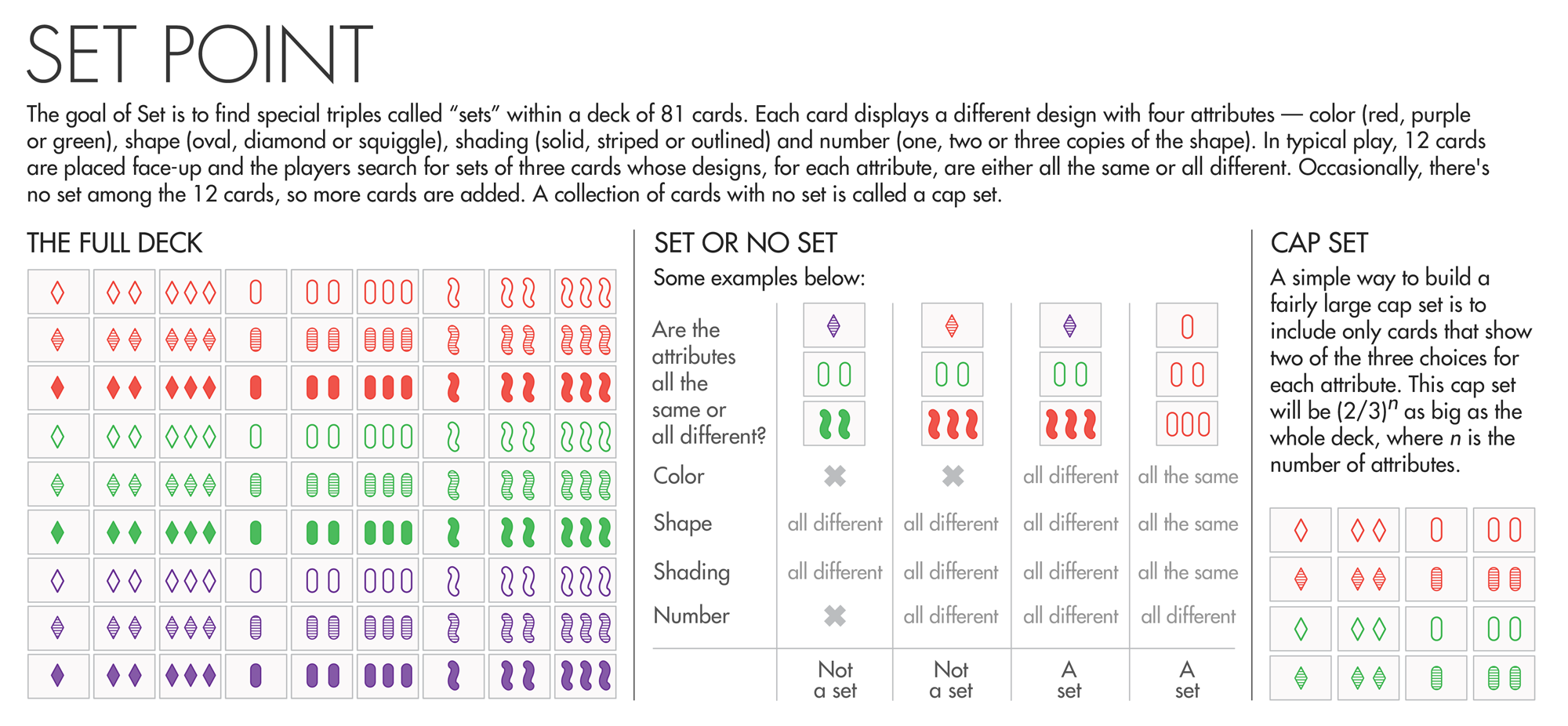
Misalkan terdapat $81$ buah kartu, dimana setiap kartu  mempunyai empat buah atribut yaitu: gambar, angka, warna, dan arsiran, dimana masing-masing atribut dapat berupa $3$ kemungkinan.

Apabila diambil 12 kartu, kemudian dipaparkan, kita diminta untuk menemukan tiga buah kartu dari 12 kartu tersebut sedemikian sehingga untuk tiap-tiap atribut pada ketiga kartu tersebut, semuanya berbeda atau semuanya sama.   Singkatnya seperti pada gambar berikut (diambil dari link yang sama) :

Tiga buah kartu yang memenuhi kondisi diatas, disebut SET.

Masalah ini dapat diintepretasikan dalam bentuk Aljabar Linear.  Setiap $81$ kartu dapat dinyatakan sebagai sebuah vektor berdimensi empat  $(a_1, a_2, a_3, a_4)$  dimana $a_i \in \{0,1,2\}$.

• $a_1$ menyatakan bentuk,  $0$ bila berbentuk diamond, $1$ bila berbentuk oval, $2$ bila berbentuk cacing.
• $a_2$ menyatakan angka,   $0$ bila ada satu buah, $1$ bila ada dua buah, $2$ bila ada tiga buah
• $a_3$ menyatakan warna, $0$ bila berwarna merah, $1$ bila berwarna hijau, $2$ bila berwarna ungu,
• dan $a_4$ menyatakan arsiran, $0$ bila tidak diarsir, $1$ bila diarsir garis-garis, $2$ bila diarsir penuh.

Sebagai contoh, $(1,1,0,1)$ berarti $a_1=1$ (oval) , $a_2=1$ (dua buah), $a_3=0$ (warna merah), $a_4=1$ (diarsir penuh), jadi kartu yang dimaksud adalah :

Dengan demikian, triple SET adalah tiga buah 4-tuple :

\[(a_1, a_2, a_3, a_4) ,  (b_1, b_2, b_3, b_4), (c_1, c_2, c_3, c_4)\]

dimana untuk tiap-tiap $i=1,2, 3, 4$ bilangan $a_i, b_i, c_i$ berbeda semua atau sama semua.

Perhatikan bahwa kita bisa menganggap $\{0,1,2\}$ sebagai sebuah lapangan hingga $\mathbb{F}_3$, dengan operasi modulo $3$.  Pandang persamaan

\[\alpha + \beta + \gamma = 0 \qquad \alpha,\beta, \gamma \in \mathbb{F}_3\]

hanya mempunyai solusi ketika $\alpha=\beta=\gamma$ atau ketika $\{\alpha, \beta, \gamma \}=\{0,1,2\}$. Dengan kata lain, ketika semuanya sama atau semuanya berbeda. 

Dari sini kita peroleh, tiga buah vektor di $\mathbb{F}_3^4$  :

\[\mathbf{a} = (a_1, a_2, a_3, a_4) ,  \mathbf{b}=(b_1, b_2, b_3, b_4), \mathbf{c}=(c_1, c_2, c_3, c_4)\]

membentuk SET jika dan hanya jika $\mathbf{a}+\mathbf{b}+\mathbf{c}=0$.   Hal ini juga berlaku secara general untuk $n\geq 4$, yakni pada vektor-vektor di $\mathbb{F}_3^n$, karena komponen mereka masih di $\mathbb{F}_3$. Yakni, apabila persamaan $\mathbf{a}+\mathbf{b}+\mathbf{c}=0$ terpenuhi maka $\mathbf{a}, \mathbf{b}, \mathbf{c}$ adalah Cap Set.


Persamaan $\mathbf{a}+\mathbf{b}+\mathbf{c}=0$ dimana $\mathbf{a}, \mathbf{b}, \mathbf{c} \in \mathbb{F}_3^n$, misalkan  $\mathbf{b}-\mathbf{a}= \mathbf{d}$. Maka $\mathbf{c}= -2\mathbf{x}-\mathbf{d} = \mathbf{x} + 2\mathbf{d}$ (karena field $\mathbb{F}_3$ mempunyai karakteristik 3).

Ini berarti himpunan triple yang memenuhi SET membentuk barisan aritmatika $\{\mathbf{a}, \mathbf{a}+\mathbf{d}, \mathbf{a} + 2\mathbf{d}\}$.

Jadi masalah :

Dari $3^n$ buah kartu,  berapa banyakkah kartu terbanyak yang bisa kita paparkan di meja, sehingga tidak ada tiga buah yang membentuk  SET?

Setara dengan masalah:

Berapa subhimpunan terbesar dari $\mathbb{F}_3^n$ yang tidak memuat barisan aritmatika tiga suku?

Masalah diatas disebut Cap Set problem.

Disini cukup natural bahwa jika kita ingin memperumum permasalahan ke lapangan $\mathbb{F}_q$, dimana ruang vektor yang dilihat adalah $\mathbb{F}_q^n$, namun perlu diperhatikan bahwa apabila kita bermain di lapangan dengan karakteristik bukan $3$, maka  syarat semua berbeda atau semua sama belum tentu setara dengan syarat $\sum a_i = 0$. Sebagai contoh
 misalkan karakteristik $5$, maka persamaan $x_1+ x_2 + x_3+x_4+x_5= 0$  belum tentu menghasilkan solusi semua sama atau semua beda,  contoh $(1,1,4,2,2)$ adalah solusi di lapangan $\mathbb{Z}/5\mathbb{Z}$.

Pada lapangan dengan karakteristik yang lebih umum , yang dimaksud masalah CAP SET adalah masalah mencari himpunan terbesar yang tidak mempunyai tiga buah suku barisan aritmatika.
Sedangkan masalah dimana semua koordinat berbeda atau semua koordinat sama itu disebut masalah sunflower.  Disini kita akan berpindah ke masalah Cap Set saja.

Pada post berikutnya, saya akan memberikan argument untuk mendapatkan batas atas dari Cap Set.